An analysis of Lewis’s celestial observations made during their stay at Long Camp near present-day Kamiah, Idaho.
Homeward Bound
The community, which had a post office in 1878, grew somewhat after 1895, when the Nez Perce Reservation was opened to white settlement. The “Heart of the Monster” was the source from which Coyote created the Nez Perce, or Nimi’ipuu people.
Spring 1806 had just arrived with the vernal equinox. Spring—the very word conjures images of warmth, comfort, family, friends, even to the most steadfast explorers. It is not surprising then that Lewis, Clark and many of the others, despite advice to the contrary, thought it was time for the expedition to start back to the “U. States.” There were more justifiable reasons for starting back, however, were: food was in short supply, trade goods were nearly exhausted and the captains thought that a change in diet and location would help the many men who were sick. On 23 March 1806, the Lewis and Clark Expedition started back up the Columbia River—toward home.
It was mostly familiar ground, and the party kept up a good pace. By 29 April 1806, the expedition was camped on Walla Walla River just upstream from its mouth and about 10 miles south of present-day “Tri-Cities,” Washington. Outfitted now with twenty-three horses, the party prepared for the overland journey from the Columbia to Lewis’s (Snake) River.
Averaging a little less than twenty miles per day, the expedition, on May 4, reached the Snake River about 8 miles downstream from the mouth of Clearwater River. After a late breakfast near the river, the expedition then headed eastward up the Snake. At the present-day Idaho-Washington border the Snake River turns south; the party, however, continued along the Clearwater River.
Establishing Camp
On 7 May 1806, about 10 miles west of their 1805 Clearwater Canoe Camp, the explorers left the river bottom and ascended the river hills to the south. Having reached the plateau, they headed east about 5 miles then turned south along the heights west of Clearwater River. After slogging all day, 10 May 1806, through several inches of fresh snow, the expedition descended a steep trail and, in the late afternoon, reached a Nez Perce village on Commearp (Lawyer) Creek less than 4 miles west of present-day Kamiah, Idaho. Here Big Arm, one of the Nez Perce chiefs, graciously invited the explorers to remain a few days as his guests.
Early in the afternoon of 13 May 1806, the expedition headed east down Commearp Creek to the Clearwater River. The party then continued north about a mile and made camp on the southwest side of the river. The next morning the men ferried equipment to the river’s right bank then swam the horses across. The captains chose a site that provided a measure of defense. This would be their camp. Here they would wait while the sun melted the snow that blocked the Lolo Trail.
Shortly after establishing themselves at their new camp, the travelers built “tents” of sticks and grass to protect themselves from the elements. The Captains’ shelter also made use of part of a sail. Though the shelter protected them to some degree from the night’s cold, it failed to keep out the heavy rain that came down during the night of 16 May 1806.
On the morning of 17 May 1806, Lewis discovered that the chronometer had gotten thoroughly wet. He opened the chronometer’s case, drained the water and attempted to dry the gears and springs with feathers. After cleaning out some rust, he put a few drops of bear’s oil on the workings to lubricate them. He then wound and reset the chronometer. Unfortunately, he didn’t specify at what time he reset it or how he derived that time.
The expedition remained twenty-seven days at this camp, but the captains—contrary to their usual custom—never gave it a name. Elliott Coues, in his edition of the expedition’s history (1893), called it Camp Chopunnish, a name which it appropriately retains[1]Long Camp is now the preferred name for this camp.—ed.
Observations
On their westward trek the captains dutifully took celestial observations at important locations. Now that they were headed back, the captains may have thought there was less need to acquire celestial data. After all, their 1806 route and campsites could be approximated from their 1805 celestial observations and the bearings and distances they took every day they traveled—no?
Perhaps that was the captains’ thought, for despite the accident to the chronometer on the 17th and despite fair weather on May 22, 23 and 24, Lewis made no effort to check and see how this important timepiece was running—at least, there is no mention of any such effort in the journals.
25 May 1806, Equal Altitudes of the Sun, Lunar Distance from the Sun
Clouds brought a light rainfall during the night but they cleared away a few hours after sunrise. Was it seeing the sun break through those parting clouds that finally prompted Lewis to make an Equal Altitudes observation of the sun. Whatever it was, the observation was long overdue and the captains put aside their “doctoring” duties that morning to make the observation. Fair weather prevailed the remainder of the day and Lewis was able to complete the afternoon part of the Equal Altitudes observation.
Lewis made no calculation to find the chronometer’s error with respect to local time. He may be excused in this, however, because he did not have the 1806 Nautical Almanac with him and he may have thought that, without the data from it, his calculations would have been incorrect. This is true, but only to a minor extent. He could have used the data from the 1804 and 1805 Almanacs to project the 1806 data sufficiently close to make this calculation.
But . . . even without that calculation—in fact, even without the Equal Altitudes observation—Lewis should have been aware that the chronometer was losing time at a much higher rate than it ever had before. Lewis’s standard procedure was to wind chronometer every day about noon, determining that time either from his pocket watch or by estimating it from the sun’s position. In doing so, Lewis (or whoever was designated to wind the chronometer) must have noted the discrepancy between solar noon and the time that chronometer showed then. By 25 May 1806, Lewis ought to have known that the chronometer had lost about 2 hours since the 17th. Additionally, Lewis certainly must have looked the chronometer times recorded for his forenoon and afternoon observations and seen how “off-balanced” they were—5:40 AM and 1:19 PM; the average should have been 12 noon, not about 9:30 AM.
Just eight minutes after the captains finished the afternoon Equal Altitudes observation, they began taking an observation of the Lunar Distance from the sun. The moon, then at its First Quarter, stood pale-white against the blue sky, about 32° high, bearing to the southeast. The sun at that time was nearly due west, over the hills west of Clearwater River, and just a little lower than the moon. Lewis would have to hold the sextant nearly horizontally to make this observation; a difficult position made more difficult by the large angle of separation of the two bodies.
Less than fifteen minutes after they began the observation, the captains had finished it and were putting away the instruments. This was the only Lunar Distance observation the captains made during the 27 days the expedition stayed at this camp.
26 May–4 June 1806
Although the weather was fair again after sunrise on 26 May 1806 and remained so all day, Lewis made no Equal Altitudes observation to find the chronometer’s error on local time. This was a substantial omission on his part because from two observations a day apart it would have been a simple matter to find the chronometer’s daily rate of loss. Then, with chronometer’s error at noon and its daily rate of loss it was an equally simple matter to find the “true” time of the Lunar Distance observation taken on the 25th.
Additionally, because the time for an observation could be calculated from the latitude and the sun’s altitude and declination, the time for the observation that was derived from Equal Altitudes observations, taken a day apart, could be used to check the calculated time and be averaged with it if necessary.
From 27 May 1806 to the afternoon of 4 June 1806 the weather remained mostly cloudy with occasional rain. There were several afternoons, especially that of 1 June 1806, when the sky cleared, but the moon, during this period, was too far from the sun for observations. Clouds, even if intermittent, might have thwarted chances for taking a Lunar Distance observation with a star, but the real reason for not taking the distance from a star was that Lewis didn’t have the 1806 Nautical Almanac, and he just wasn’t that certain of his star identifications without the information in that almanac.
5 June, Equal Altitudes and magnetic declination
Finally, a clear morning after so many cloudy ones! Bartering for food would have to wait while the captains took another Equal Altitudes observation. There would be plenty of time for bartering between the forenoon and afternoon observations.
If (unlikely as it may be) Lewis hadn’t already known about the chronometer’s error with respect to local time, he certainly would have with this Equal Altitudes observation. The mid-time for the forenoon observation by the chronometer was about 3:09 AM and the mid-time for the afternoon observation was 11:41 AM! Even a quick mental calculation would reveal that the chronometer was about 4 hours and 35 minutes slow on Local Apparent Time.
Eleven minutes after the captains completed the afternoon Equal Altitudes observations, they began taking an observation of the sun to determine the Magnetic Declination (Variation of the Compass Needle). A little more than six minutes later they took a second observation. The chronometer at that time showed it to be noon, in reality, it was about 4:35 PM.
6 June Equal Altitudes of the sun
A fair morning. The captains took advantage of this opportunity to take a next-day Equal Altitudes observation and discover the chronometer’s true rate of loss! After the forenoon observation clear skies continued, allowing the captains to complete the afternoon observations. Lewis left no record of any calculations made to determine the chronometer’s error and rate, but it is likely that he made at least a rough calculation.
To make this calculation all he would have needed to do is: 1) take the average of the mid-time of the forenoon and afternoon observations for the 5th; 2) take the average of the mid-times for forenoon and afternoon observations for the 6th and 3) subtract the average time on the 5th from that of the 6th. Doing so, he would have discovered that the chronometer’s daily rate of loss—at least for the interval between those two observations—would have been about 1h 17m!
9 June, Meridian Observation of the sun
Why did Lewis wait until just one day before the expedition left this camp for Weippe Prairie to take a Meridian Observation for latitude? He certainly knew how critical it was to have a “good” latitude upon which to base almost all other astronomical calculations at a site.
Perhaps Lewis was uncertain about his octant, especially its index error. On 16 February 1806, Lewis recorded that there was a fracture on one of the octant’s limbs and gave its index error when used in the “fore” method. On 9 June he finally noted the octant’s index error when used in the “back” method, but only for that part of the limb “beyond” the fracture. Did Lewis know, for sure, what the index error was for that part of the limb “below” the fracture? Was it the same as he recorded on 22 July 1804? Did he trust using the octant? It seems, at least, that he was reluctant to do so.
In Lewis’s defense it is well to remember that the previous October, he and Clark, despite being sick, took many celestial observations at a site which, by now, they knew to be only 20 or 30 miles north of this camp. Lewis may have figured that the latitude at this camp could be determined fairly closely by using both: 1) the latitude they had determined with the sextant for their canoe camp and 2) the courses and distances they recorded while traveling to this site from where they left Clearwater River on 7 May 1806 and would record on their way back to Weippe Prairie.
Lewis could not use the sextant to take the Meridian Altitude of the sun while at Camp Chopunnish because the sun’s noon altitude exceeded 60°, but he made an important statement about it—also on 9 June. On that date Lewis recorded that the sextant’s index error was 6’15” “subtractive”[2]That is, the sextant read too high by that amount. Thus, that value had to be subtracted from any observation made with the sextant. What caused this change of 2’30”? When? instead of the 8’45” it had been previously. It should be noted that Lewis, on 4 February 1806, recorded that the sextant’s index error was 5’45”, but this value, most likely, is a transcription or copy error for 8’45”.
Summary
Weather, lack of an 1806 Nautical Almanac, the need to stay atop a multitude of pressing daily situations and the logistics of command all interfered with Lewis’s opportunities to take celestial observations while at Camp Chopunnish. Still . . . he seems to have missed a number of excellent opportunities to take needed observations.
Clark’s “doctoring” may have taken a large amount of his time, and he did draw several maps from Nez Perce sources while at Camp Chopunnish, but he never made a detailed plot of the expedition’s route from the Columbia to this camp, nor did he plot it on any of the detailed maps he had made previously. The only surviving map Clark made that shows the location of this camp is that in his field notebook (Moulton, Journals, 7:317). Using the map in his field notebook and projecting it onto the Lewis and Clark Map of 1806 gives the approximate coordinates of Camp Chopunnish as 46°15’N, 116°30’W. The coordinates of the camp, determined from map interpretation and information from Olin D. Wheeler in 1902,[3]Olin D. Wheeler, The Trail of Lewis and Clark, 1804-1806 (New York: G. P. Putnam’s Sons, 1904), 268-71. are 46°14’31″N, 116°02’04″W.
Considering the problems with the chronometer and the octant, and the changed index error for the sextant, can anything useful be made of the few celestial observations the captains made while at Camp Chopunnish?
Latitude
Octant and Meridian Altitude of the sun
Calculations of celestial observations usually begin with determining the latitude of a point of observation, especially if the data were obtained from a Meridian Altitude observation of the sun. Lewis waited until 9 June, the day before leaving Camp Chopunnish, to make this necessary observation and, because of the sun’s noon altitude, he had to take the observation with the octant by the “back sight method.”
The angle that Lewis recorded for this observation, however, was not the sun’s altitude; it was the supplement of the double altitude of the sun’s lower limb. This means that the angle he observed had to be subtracted from 180° then divided by two to find the “observed” altitude of the sun’s lower limb.[4]Lewis first would divide the observed angle by 2, then subtract the result from 90°. Both his method and that given above produce the same answer, though the one above is procedurally more … Continue reading From the “observed” altitude it still was necessary to subtract the effect of refraction, add the effect of parallax and add the sun’s semidiameter; the “sum” of these three operations was the altitude of the sun’s center. Having mathematically determined the true altitude of the sun’s center it was then necessary to algebraically subtract the sun’s declination from it. Having completed that operation, subtracting the result from 90° gives the calculated latitude (for the calculations.
Using the index error for the octant that Lewis gave on 22 May 1804 and which he reaffirmed while at Fort Clatsop (see Fort Clatsop Miscellany), his observed angle yields a latitude of 46°09’12” N. The actual latitude of Camp Chopunnish determined from information in the courses and distances and from early sources who identified the camp’s location is 46°14’31″—a difference of 5’19”. This difference of 5’19” is larger than any of the differences between the actual latitude and the latitude recalculated from observations that Lewis made in 1805. The difference might result from a changed index error or from the fact that Lewis had not taken an observation with the octant since August 1805. In any case, the difference is not much greater than for many observations taken for latitude at sea at that time.
Sun’s altitude, declination and hour angle
Theoretically, it is possible to calculate a latitude from the data derived from any observation in which one knows the sun’s altitude, its declination and its hour angle (that is, the difference between the Local Apparent Time of the observation and noon— multiplied by 15).
Equal Altitudes observations normally provide all that data, but the observation for 25 May was not followed by an observation the next day, so the chronometer’s rate-of-going is uncertain. The Equal Altitudes observations for 5 June 1806 and 6 June, however appear to provide the data necessary to determine the rate. At noon on 5 June the chronometer was 4h 33m 11s slow on Local Mean Time and on 6 June it was 5h 50m 22s slow—a loss of 1h 17m 11s in 24 hours! The question is, did the chronometer stop or change rate between the two observations or did it run at a steady rate?
This exceptionally high rate-of-loss, at first, doesn’t inspire much confidence in a calculation for latitude from chronometer’s time. Nevertheless, by plotting the chronometer error for 5 June and 6 June and projecting its rate-of-loss of 1h17m per 24 hours back to 25 May, one discovers that the line passes close to the chronometer’s error at noon on 25 May—provided 12 hours are subtracted from that error (that is, at a rate-of-loss of about 1h17m per day, the chronometer had lost more than 14 hours in eleven days). This is an unbelievably high daily rate-of-loss, but the near-concordance of times suggests that the chronometer had been running at nearly a steady rate during this period of time. It would be unwise to make any calculation from the Equal Altitudes observation on 25 May because the projected line, although passing close to the chronometer’s error at noon determined from that observation, still misses by too far to warrant that calculation. It does appear reasonable, however, to attempt a calculation from the time given by PM observation on 5 June and that of the AM observation on 6 June.
Unfortunately, the calculations, once made, show that Lewis took both the Equal Altitudes observations at a time when the sun was nearly east or west. Therefore, the last step of the equation for determining the latitude as given in Robert Patterson‘s Astronomy Notebook, Problem 1, “falls apart.” The problem is that the arc-cosine needed to complete the calculation is too near unity to give reliable results.
Fortunately, Lewis took two observations for Magnetic Declination between the PM Equal Altitude observation on and the AM Equal Altitudes observation on 6 June. Even though these observations for Magnetic Declination shortly followed the PM observation on 5 June, the sun would have moved farther to the north of west away from the 0°-90°-problem. The calculations for the first Magnetic observation produce a latitude of 46°10’37″N, seeming to confirm the octant latitude. The second Magnetic observation, however, produces a latitude of 46°20’41″N. The average of these two calculations is 46°15’39″N, but can an average from such divergent results be trusted?
As noted above in the Summary on page 3, above, the latitude of Camp Chopunnish can be approximately determined on the Lewis and Clark Map of 1806 (Moulton, Atlas, map 123) at about 46°15′ North.
Magnetic Declination
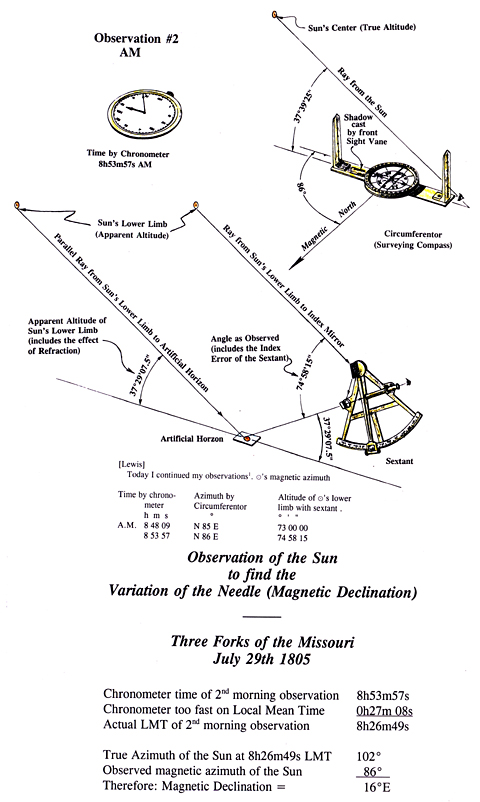
Lewis took two observations for Magnetic Declination six minutes apart after taking the PM Equal Altitudes observation on 5 June. The time of the observations can be determined either from 1) the chronometer error at noon on the 5th and 6th or 2) by calculating the observation times from a) the octant latitude, b) the sun’s estimated declination and c) the sun’s observed altitude. Both methods produce times within several seconds of each other—a good check on the data.
The circumferentor (a 6-inch-diameter surveying compass) used to measure the bearing of the sun during this observation could be read only to the nearest½ arc minute. In addition, it is difficult to aim the surveying compass’s sighting vanes directly at the center of the sun, even if using smoked glass to block the sun’s glare. These difficulties can either re-enforce each other and make the reading worse or compensate for one another and result in a “good” observation.
During the observations, the sun’s bearings obtained from the surveying compass were S76°W and S77°W. These bearings can be converted to azimuths of 256° and 257°, respectively. Using the octant latitude, the sun’s declination and the sun’s hour angle,[5]Hour angle = the difference in time from noon in hours ◊ 15. the true azimuth of the sun at that time can be calculated.[6]Sine½ azimuth = {√ [cosine½ (z + l + d) ◊ sine½ (z + l—d)] ˜ (sine z ◊ cosine l)} where z = zenith distance (90°—sun’s true altitude), l = … Continue reading For the first observation the Magnetic Declination turns out to be 17°10’50″E and for the second 17°22’45″E. Because most hand-held compasses can be read only to the nearest degree, the results of these observations could be reported simply as 17°E.
At first glance the magnetic declination here of 17°E is something of a surprise considering that the captains’ observations in October 1805 at Clearwater Canoe Camp, less than 25 miles to the northwest, produced an average magnetic declination of 18½°E. The difference may have been caused by local magnetic anomalies, including the expedition’s knives, rifles, and other equipment, or even from iron-rich basaltic rocks, especially at Clearwater Canoe Camp.
Determining Time of the Observation
Lewis had a number of opportunities for taking Lunar Distance observations for longitude other than the one he took on 25 May, but duties of command, weather and lack of an 1806 Nautical Almanac hampered his attempts. Because Lewis did not take an Equal Altitudes observation on the 26th (or even the 27th), the time of the observation on 25 May is a problem.
There are two ways to try to resolve this problem. The first is to take the chronometer errors at local noon on 25 May, 5 June, and 6 June and plot them to derive the chronometer’s rate of loss. If there was a good correlation one might assume that the rate-of-loss was constant, and from this one could make an approximation of the mean or mid-time of observation. The problem is that, although the line between the three points so plotted is close to a straight line, it doesn’t pass through the time for which the chronometer was set on 17 May (assuming that it was set at local noon as it should have been). Additionally, a gap of eleven days between observations and a loss rate of 1 hour 17 minutes per days is a tenuous thread upon which to hang so important a calculation as the longitude.
The second method of deriving the true mean or mid-time of the observation is to calculate the time of the forenoon and afternoon Equal Altitudes observations on 25 May and compare them with the times shown by the chronometer. Next, these times are graphed or put into a linear regression together with the time the chronometer would have shown at noon based on its error at noon. This method also presents problems arising from uncertainties about the sextant’s index error, and from the accuracy of the sun’s observed altitude, but is the “safer” of the two methods to use.
The large observed angular distance between the sun and the moon of about 102½° is the yet another sign of trouble with this Lunar Distance observation. This is because observations with separations much over 90° are more difficult to take than those, say, between 40° and 80°. Still, with a steady hand and good eye they can provide an acceptable longitude.
The long and exacting preparatory calculations would have been considerably shortened and simplified if the captains had done two things. The first of these would have been to take another observation for Equal Altitudes on 26 May or 27 May to determine the chronometer’s rate-of-loss more nearly. The second would have been to measure the altitude of the sun and moon at the beginning and end of the time-distance measurements. This, alone, would have made Steps 3 and 4, below, unnecessary.[7]At sea, with multiple sextants available and other personnel trained in making observations also available, these altitudes were regularly taken. On land, however, with a single sextant and using an … Continue reading
Preparatory Calculations
Step 1
The first step is to take the recorded chronometer times for the observation and plot them against the observed angular separation of the sun and moon’s nearest limbs. The plot reveals there is a large time gap between the first and second data sets. The first data set should be omitted. The plot also reveals that there is an error with the fourth data set: the time is later than for the next data set. The time for the fourth data set, in reality, appears to be 1:38:34, not 1:39:34, but it is best to omit this set, too, because data sets 2, 3, 5 and 6 make nearly a straight line. The average chronometer time for the four “good” data sets is 1:38:15 PM and the average angular sun-moon separation for those same four data sets is 102°29’15”.
Step 2
Second, find the true Local Apparent Time of the observation. In the discussion on latitude above it has been seen that by projecting the chronometer error backwards from 6 June through 5 June to 25 May that the chronometer’s rate of loss for 25 May falls close to the resultant line, but for a lunar distance observation, close isn’t good enough.
A calculation using an “average” latitude of 46°13’30” (derived from the meridian altitude observation of 9 June and the mean of the latitude from the two observations for Magnetic Declination—see Latitude, above) produces a “true” Local Apparent Time of 7:58:17 for the AM Equal Altitudes and a “true” Local Apparent Time of 4:01:57 for the PM Equal Altitudes. From these times and the chronometer error at noon, the “true” Local Apparent Time of the mean of the Lunar observation turns out to be 4:22:45 PM.
Step 3
Now it is necessary to determine the hour angle of the sun. This is merely the hour-minutes-seconds of the observation times 15; the hour angle thus is 67°41’15”. From this hour angle, the latitude and the sun’s estimated declination, the calculated the true altitude the sun’s center turns out to be 31°37’37”. But, to make the calculation by the methods of the time, it is necessary to determine what the “observed’ altitude might have been—to “uncorrect” the observation as it were; that is, add back in the effects of parallax and refraction. This operation produces an altitude of 31°39’00” for the sun.
Step 4
Fourth, using the 1806 Nautical Almanac, one obtains the Right Ascension of the sun for Greenwich noon on 25 May and 26 May and from the estimated longitude of the camp, determines the sun’s Right Ascension at the time of the observation. This procedure is followed by obtaining the moon’s Right Ascension for noon and midnight of 25 May and determining its Right Ascension for the time of observation. Next the sun’s Right Ascension is subtracted from that of the moon, giving the moon’s hour angle. Continuing on, one obtains the moon’s declination for noon and midnight from the Nautical Almanac and calculates the moon’s declination at the time of observation. The hour angle, declination and latitude produce a true altitude of 33°42’02” for the moon’s center. The moon’s true altitude also must be “uncorrected” to what the captains might have observed. This is a more complicated operation because the moon’s parallax is so great and usually changes at a rate arc seconds per hour. But finally the calculation is made and the “observed” altitude comes out to be 32°54’04”.
Step 5
There are still more calculations to be made before the true distance can be computed. The sextant’s index error of 6’15” needs to be subtracted from the observed distance (102°29’15″—6’15” = 102°23’00”). To this the sun’s and moon’s semidiameter (calculated from data in the Nautical Almanac) are added, and also the moon’s augmentation (derived also from the Tables Requisite). Now we are ready to begin the calculations to determine the true distance of the sun from the moon and then the longitude.
The data produced above are entered onto a form using a procedure essentially identical to that outlined by Robert Patterson, though modified to use real numbers instead of the logarithms that would have been used at the time.
Testing Patterson’s formula
| A = | Apparent angular distance center of the Moon to center of the Sun = Observed mean distance – Index Error + sun’s semidiameter + moon’s semidiameter + moon’s augmentation = 102°29’15" – 6’15" + 15’48" + 16’01" + 8" = |
102°54'58.5" |
| B = | Moon’s "observed" altitude = | 32°54'04" |
| C = | Sun’s "observed" altitude = | 31°39'00" |
| D = | 1⁄2 (B+C) = 1⁄2 (32°54’04"-31°39’00") = 1⁄2 (64°33’04") = | 32°16'32" |
| E = | C+ Å`D = 31°39’00" – 32°16’32" = | 0°37'32" |
| F = | A ÷ 2 = 102°54’58" ÷ 2 = | 51°27'29.25" |
| G = | tan-1 tangent D x cotangent E x tangent F = tan-1 tan 32°16’32" x cot 0°37’32" x tan 51°27’29" = tan-1 0.63157678 x 91.5881929 x 1.255284945 = tan-1 72.61192752 = |
89°12'39.5" |
| H = | F ± G =F – G = 51°27’29.25" – 89°12’39.5" = | 37°45'10.2" |
| I = | F ± G =F + G = 51°27’29.25"+ 89°12’39.5" = | 140°40'08.8" |
| K = | proportional log (180 ÷ moon’s horizontal parallax = 180 ÷ 58’47.8" = | 3.060891915 |
| L = | proportional log (180 ÷ cosecant B x tangent I x K = 180 ÷ cosecant 32°54’04"x tangent 140°40’08.8" x 3.060891915 = 180 ÷ 1.840973972 x 0.819391192 x 3.060891915 = 180 ÷ 4.61728768 = 38.98392573 = |
38'59.0" |
| M = | refraction of I = ref of 180°-140°40’08.8 = ref of 39°19’51.2" = | 1'06.7" |
| N = | L – M = 38’59.0" – 1’06.7" = | 37'52.3" |
| O = | A – N = 102°54’58.5" – 37’52.3" = | 102°17'06.2" |
| P = | refraction + parallax of H =ref + par of 37°45’10.2" = | 1'03.6" |
| Q = | O + P = 102°17’06.2" + 1’03.6" = | 102°18'09.8" |
| R = | Tables Requisite (can be ignored) | 102°18'10" |
| S = | true distance = | 102°18'10" |
Notes
| ↑1 | Long Camp is now the preferred name for this camp.—ed. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ↑2 | That is, the sextant read too high by that amount. Thus, that value had to be subtracted from any observation made with the sextant. What caused this change of 2’30”? When? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ↑3 | Olin D. Wheeler, The Trail of Lewis and Clark, 1804-1806 (New York: G. P. Putnam’s Sons, 1904), 268-71. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ↑4 | Lewis first would divide the observed angle by 2, then subtract the result from 90°. Both his method and that given above produce the same answer, though the one above is procedurally more correct.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ↑5 | Hour angle = the difference in time from noon in hours ◊ 15. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ↑6 | Sine½ azimuth = {√ [cosine½ (z + l + d) ◊ sine½ (z + l—d)] ˜ (sine z ◊ cosine l)} where z = zenith distance (90°—sun’s true altitude), l = latitude and d = sun’s declination. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ↑7 | At sea, with multiple sextants available and other personnel trained in making observations also available, these altitudes were regularly taken. On land, however, with a single sextant and using an artificial horizon for altitude, the process is considerably more difficult to manage. Besides, Robert Patterson recommended that, on land, the “observed” altitudes be calculated. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ↑8 | Thomas Jefferson asked Robert Patterson (1743-1824), professor of mathematics at the University of Pennsylvania, to help Lewis develop his skills in making celestial observations. Jefferson wrote to Patterson on 2 May 1803: “He [Lewis] has been for some time qualifying himself for taking observations of longitude & latitude to fix the geographical points of the line he will pass over, but little means are possessed here [in Washington City] of doing that; and it is the particular part in which you could give him valuable instruction, & he will receive it thankfully & employ it usefully.” For the use of his pupil Patterson wrote an instruction manual now known as the Astronomy Notebook. Donald Jackson, Letters of the Lewis and Clark Expedition with Related Documents, 1783-1854 (2 vols., Urbana: University of Illinois Press: 1978), 1:21, 28-31. |
Experience the Lewis and Clark Trail
The Lewis and Clark Trail Experience—our sister site at lewisandclark.travel—connects the world to people and places on the Lewis and Clark Trail.
Discover More
- The Lewis and Clark Expedition: Day by Day by Gary E. Moulton (University of Nebraska Press, 2018). The story in prose, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals: An American Epic of Discovery (abridged) by Gary E. Moulton (University of Nebraska Press, 2003). Selected journal excerpts, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals. by Gary E. Moulton (University of Nebraska Press, 1983–2001). The complete story in 13 volumes.