The Kansas Meets the Missouri
To see labels, point to the image.
Library of Congress, Geography and Map Division, Washington, D.C.
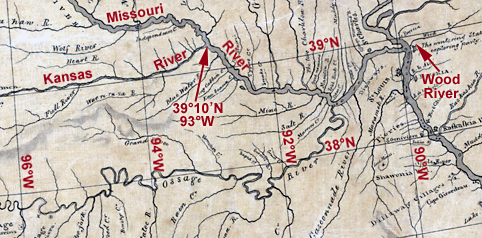
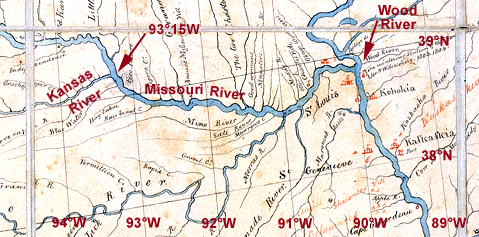
The coordinates at the mouth of the Kansas River today, at the mid-point between its right and left banks where it touches the Missouri’s right bank, is 39°06’56” N; 94°36’36” W. The point where the centers of the two rivers intersect is at about 39°07’N.
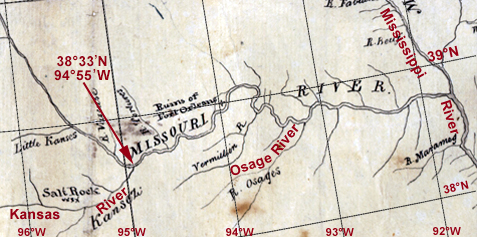
Early in 1803 Albert Gallatin and Thomas Jefferson commissioned the Philadelphia cartographer Nicholas King to create a new chart for Lewis’s use as a base map. The result was a compilation of details from at least seven or eight other 18th-century maps containing what was then believed to be the best geographical information about North America west of the Mississippi and between 30° and 55° north latitude. King’s most recent source was the 1802 map by the British cartographer Aaron Arrowsmith, who relied partly on the explorations of Peter Fidler. On the King map the mouth of Kansas River can be interpreted to be at 38°18′ N, 94°55′ W; this places it 58 miles south-southwest (azimuth 197°) from its actual location (39°06’54” N, 94°36’36” W). The King map also shows the Missouri to make a sharp bend to the northwest at the mouth of the Kansas, and this northwest course continues to the Mandan villages. Both the size of the Kansas River and the change in direction of the Missouri’s course influenced the captains to take the necessary astronomical observations at this junction.
On a rainy Monday afternoon, 14 May 1804, the “Detachment destined for the Expedition through the interior of the Continent of North America,” embarked in a military barge (called the ‘boat’ or ‘barge’ but never the ‘keelboat’) and two pirogues from the mouth of Wood River in the Illinois country, and headed up the Missouri River. William Clark, in sole command—until joined by Meriwether Lewis a few days later in St. Charles—logged a mere four miles before making camp for the night. Six weeks and about 350 river miles later, in the afternoon of Tuesday 26 June 1804, these three teams of boatmen, duly seasoned by six weeks of practical experience, arrived at the mouth of the Kansas River.
At various stops along the Missouri River’s nearly east-west general course up to that point, Lewis and Clark, in accordance with President Thomas Jefferson’s instructions, had taken four different types of celestial observations. These were:
- Equal Altitudes of the sun to check the chronometer (seven separate observations, each consisting of six sets of measurements of the sun’s altitude, and the times of the observations);
- Meridian Altitude observation of the sun for latitude (twelve measurements);
- Bearing and altitude of the sun and the time (five observations to determine the magnetic declination[1]Magnetic declination, also called variation of the needle, is the difference in degrees between Magnetic North, which is the direction the needle of their magnetic compass pointed, and True North. … Continue reading); and the
- Lunar Distance from the sun or a star for ultimately calculating longitude. These observations were made at four places and consisted of a total of ninety-four separate angular readings. The captains did not calculate longitudes themselves, but after returning home sent the data to Ferdinand Hassler, the mathematician then at West Point.
Altogether, these four types of observations added up to a total of at least 153 different angular measurements.
From maps that the captains had studied during the winter of 1803-04, and from information given them by knowledgeable people around St. Louis, the captains recognized the importance of this river junction. The Kansas River reached westward nearly to the Rocky Mountains and, along it, there lived Indians whose trade and commerce could provide impetus to cultural exchange, the benefits of which could be important both to those native nations and to the fledgling United States. Equally important, but from a geographic point of view, at this confluence the Missouri, having flowed generally toward the southeast for more than 650 miles from the vicinity of the Mandan Indian villages, abruptly turned eastward. Unmistakably, this was one of those “remarkable points” where Jefferson wished Lewis to take celestial observations in order to refine the sets of day-to-day travel measurements they had estimated.[2]Jefferson had instructed Lewis to base their estimates of distances traveled on waterways “by the compass the log-line & by time.”Lewis listed “Log line reel & log … Continue reading
Schedule of Observations
Celestial observations at this junction began shortly after 8 a.m. on 27 June 1804. The first observation would provide the data necessary to calculate the magnetic declination at this junction. One observer used the six-inch diameter magnetic compass (circumferentor) and took the sun’s bearing while another observer measured the sun’s altitude using the sextant and an artificial horizon. A third person recorded the chronometer time for each set of bearings and altitudes.
Moments after completing the observations for magnetic declination, the captains began taking the a.m. set of observations of Equal Altitudes of the sun. Following the p.m. set of Equal Altitudes observations, they could make calculations that would show how fast or slow their chronometer had been at noon compared with Local Time. Between the a.m. and p.m. sets of observations, Lewis took an observation of the sun’s noon altitude with the octant and artificial horizon to determine the latitude of the mouth of Kansas River.
Observations continued until late at night on the 27th, and more followed the next day. The captains took their last celestial observations at this junction in the afternoon of 29 June 1804 just before continuing upriver. These are the fourteen sets of observations they took:
| Date | Type of Observation |
|---|---|
| 27 | Magnetic Declination with the Sun |
| 27 | Equal Altitudes of the Sun, a.m. |
| 27 | Meridian Altitude of the Sun |
| 27 | Equal Altitudes of the Sun, p.m. |
| 27 | Magnetic Declination with the Sun, p.m. #1 |
| 27 | Magnetic Declination with the Sun, p.m. #2 |
| 27 | Magnetic Declination with Polaris |
| 28 | Equal Altitudes of the Sun, a.m. |
| 28 | Meridian Altitude of the Sun |
| 28 | Equal Altitudes of the Sun, p.m. |
| 29 | Lunar distance from the Sun observations 1—6 (8 sets of distance and time for each) |
| 29 | Equal Altitudes of the Sun, a.m. |
| 29 | Meridian Altitude of the Sun |
| 29 | Equal Altitudes of the Sun, p.m. |
Navigational Mathematics
After returning to St. Louis in September 1806, Lewis sent some of the Expedition’s celestial observations and a payment in advance to mathematician Rudolph Hassler in Schenectady, New York, for work Jefferson had asked him to undertake, the Astronomy Notebook. It is probable that Hassler was expected to make only the calculations that would yield longitudes from those observations. This interpretation comes from a letter Hassler wrote to astronomer-mathematician Robert Patterson in 1810,[3]Ferdinand Rudolph Hassler to Robert Patterson, 12 August 1810, in Donald Jackson, Letters of the Lewis and Clark Expedition with related documents 1783-1854 (Urbana: University of Illinois Press, … Continue reading Hassler does not mention latitudes or magnetic declination in that letter, but he specifically describes problems with the longitude information and also describes ambiguities, uncertainties and mis-calculations in the original data. One of Hassler’s principal impediments was the lack of a detailed map showing where the observations were taken; another is the absence of adequate information about the equipment used and the captain’s method of taking and recording their observations. Undoubtedly, Hassler made a sincere effort at calculating some of the longitudes, but Clark never received any information from him for the observations that he and Lewis took—coordinates that would have helped place key points on the map that ultimately accompanied the 1814 Nicholas Biddle edition of their journals.
Lewis calculated (and sometimes miscalculated) most of the latitudes from observations of the sun’s noon altitude in 1804 and 1805, but no one—within the lifetime of Lewis, Jefferson or Clark—is known to have successfully calculated all geographic data from the other observations the captains made. Only with the onset of the Lewis and Clark Bicentennial were any of these other calculations made.[4]See, for example: Richard Preston, “The Accuracy of the Astronomical Observations of Lewis and Clark,” Proceedings of the American Philosophical Society, vol. 144, no. 2 (June 2000), … Continue reading
A Conjecture
While in Pennsylvania during the spring of 1803, Lewis received a hasty education in taking and recording the celestial observations Jefferson ordered him to make on the expedition. (The only observation he knew how to take before his meeting with Andrew Ellicott was that for the meridian observation of the sun, which he learned from Jefferson.) Undoubtedly, Lewis also received some training on how to make the necessary calculations to turn those observational data into latitude, longitude, time, altitude and direction. Suppose, however, that instead of just being taught the basics, his training had been thorough, giving him the competency to correctly calculate all his celestial observations, converting them into geographical information with an accuracy comparable to that of the better maritime navigators of his day. Suppose further that Lewis, when he was at Fort Mandan, had found the time to calculate or re-calculate all the observations he had taken up to that point.
These conjectural calculations of Lewis’s would have been made using five-place logarithms and “note book” methodology following procedures devised by persons such as Robert Patterson or Andrew Ellicott. In addition, his initial calculations, which required only an estimation of his longitude, would have depended upon the geographical information he had available. Consequently, the latitude, longitude and magnetic declination obtained by his calculations would, in most cases, have differed somewhat from what might be obtained nowadays. The object here is to discuss and evaluate the geographic data that might have been derived at the time of the Expedition.
Latitude
Of all the celestial observations the captains took, the simplest to calculate is the latitude from a meridian (noon) observation of the sun. Let’s assume these calculations would be made first. There were a number of different ways to make them but, assuming the mathematics were correct throughout, the results should be essentially the same. Lewis’s method appears to have been as follows: Example from Lewis’s Meridian Altitude observation, 27 June 1804, mouth of Kansas River:
| Observed complement of the sun’s double altitude | 36° 25′ 00″ | |
| Step 1 | Divide the angle observed by 2 (the artificial horizon doubled the angle) | 18° 12′ 30″ |
| Step 2 | Subtract the result of Step 1 from 90° (angle observed is the complement) | 71° 47′ 30″ |
| Step 3 | Add the octant’s index error (actually half its error of 2°11’40”) | 73° 59′ 10″ |
| Step 4 | Go to Tables Requisite with the angle from Step 3, find the correction for refraction for that angle (15″) and subtract it from the angle in Step 3 | 73° 58′ 55″ |
| Step 5 | Go to Tables Requisite with the angle found in Step 3 and find the correction parallax (2″), then add that correction to the result of Step 4 | 73° 58′ 57″ |
| Step 6 | Go to the Nautical Almanac and from it, determine the sun’s semidiameter for the day of the observation (15’47”), then add that value to the result of Step 5 (add the semidiameter here because Lewis shot the sun’s lower limb (bottom tangent?); with the sextant he commonly shot the sun’s upper limb) | 74° 14′ 44″ |
| Step 7 | Determine the sun’s declination . . . | |
At this point Lewis needs to know his approximate longitude; a good estimate will do—call it a “dead-reckoned” longitude. From it he can determine the approximate Greenwich time of the observation, and with that he can determine the sun’s approximate declincation[5]Except at the summer and winter solstice, the sun’s declination—that is, its angular distance north or south of the celestial equator—is constantly changing. The Nautical Almanacs of Lewis … Continue reading at the moment ofhis observation. This determination is necessary because the Nautical Almanacs of his day gave the sun’s declination only for Local Apparent (solar) Noon at Greenwich, and the sun’s declination, except at the solstices, is constantly changing.
Suppose, for example, Lewis had taken an observation of the sun’s altitude at noon on 1 May 1804 at Camp Dubois, which was at about 90° West, or 6 hours’ difference in time from Greenwich. Suppose further that he had used the sun’s declination for Greenwich noon instead of adjusting that declination for the six-hours’ difference in time. Had he done so, his calculated latitude would be too far north by 5 miles.
Step 7a . . . Lewis would have had several means by which to estimate the longitude of the junction of the Kansas and Missouri Rivers. From his own observations he had determined Camp Dubois to be at or near 38°55’20″N, and about 90° west (89°57’45” by astronomical observations and 90°00’20” by chronometer). Lewis also had information that Thomas Jefferson had obtained from British sources regarding the Mandan villages. These villages, as determined through celestial observations made by the British explorer David Thompson in 1798, were at or near 47°17’22” North Latitude, 101°14’24” West Longitude.
The coordinates of Camp Dubois and Fort Mandan, thus, could be used as anchor points between which Clark could fit the maps of the Missouri that he had plotted from the Expedition’s river survey. If Clark had used this method (which he clearly did not), the mouth of Kansas River should have been plotted at about 94° West Longitude.[6]See Clark’s map of 1805, Moulton, ed., Atlas, Map 32a. Clark probably prepared this map either by re-plotting their river survey at a smaller scale (1 inch = 100 miles) or redrafting the … Continue reading
The King map of 1803 that Lewis carried, however, showed the mouth of Kansas River at 94°55′ West Longitude. Lewis, for his first approximation of longitude, could pick an average longitude of 94°30′ for his calculations.
The nautical almanac gives the sun’s declination for apparent noon at Greenwich. Lewis, using an estimated longitude of 94°30′ W for the mouth of Kansas River, must determine what the sun’s declination would be at 6:18 p.m. Greenwich Apparent Time for each of his noon observations. On 27 June, for example, the sun’s noon declination at Greenwich by the 1804 Nautical Almanac was 2°20′ 59″ north. On the 28th at noon it was 23°18′ 23″. The difference in 24 hours apparent time is 2’36”. In the 6h18m since noon at Greenwich, then, the sun’s declination would have decreased by 41 seconds, making the sun’s declination at noon at the mouth of Kansas River 23°20′ 18″:
| Step 8 | Subtract the value for the sun’s declination from altitude obtained in Step 6, above | 50° 54′ 26″ |
| Step 9 | Subtract the result of Step 8 from 90° = latitude per this observation | 39° 05′ 34″ |
After all three meridian observations have been recalculated, the results are:
| Recalculated Latitude | 1804 Calculated Latitude (rounded) | |
|---|---|---|
| 27th | 39° 05′ 34″ | 39° 05′ 39″ |
| 28th | 39° 05′ 51″ | 39° 05′ 26″ |
| 29th | 39° 05′ 15″ | 39° 05′ 21″ |
| Average | 39° 05′ 33″ | 39° 05′ 29″ |
The average difference of four seconds between the recalculated latitude and that from the calculations made at the mouth of Kansas River stems from the estimated longitude and from a possible error on the 28th. The octant, it should be remembered, could be read only to the nearest 30 arc seconds, so both values actually become 39°05½’ North Latitude. After having calculated the chronometer’s error for 27, 28 and 29 June 1804, Lewis probably also would attempt to calculate the latitude of the mouth of Kansas River from the time and altitude of the sun obtained during the Equal Altitudes observations or from the observations for magnetic declination. After checking these observations he would find that, for most of them, the sun had been too far from the meridian or else was too close to bearing either east or west.
Nevertheless, Observation No. 3, the second p.m. observation for Magnetic Declination with the Sun taken on 27 June might provide a useful latitude. The calculations yield a latitude of 39°14’59”, but the sun likely was too far west of the meridian at the time, and accuracy deteriorates with time and angular distance from the meridian. On the other hand, the result—derived from the magnetic declination—suggests that latitude derived from the average of his three meridian altitudes of the sun is good.
Suppose that, after having calculated the longitude for the mouth of Kansas River from his Lunar Distance observations on 29 June 1804, Lewis had found that the difference between calculated longitude and dead-reckoned longitude was a degree or slightly more. Would he use the longitude from his Lunar Distance observation to recalculate the latitudes? Probably not, because at this time of year the sun’s declination is changing only about 3 arc minutes per day, and even several degrees difference between longitudes would make little change in the recalculated latitude.
By comparing the Expedition’s river survey with the oldest detailed maps and with modern maps and aerial photos, the mouth of the Kansas River in 1804 was at or near 39°07’N, 94°36½’W. The expedition’s river survey, made by using compass bearings and estimated distances, even when corrected to True North (see Magnetic Declination) puts the mouth of the river at 39°29½”N (and 94°54″W)—30 miles too far north of its actual latitude. The average latitude of this junction, recalculated from Lewis’s observations of the sun’s Meridian Altitude with the octant, is 39°05½’N. This latitude is 1½’ (just 1¾ miles) south of the redetermined latitude of 39°07’N. The positional accuracy (at least as to latitude) that could be obtained even by an instrument as imprecise as the octant justifies Jefferson’s instructions to take celestial observations to correct the ground survey—the Courses and Distances—the captains made with compass bearings and estimated distances.
Local Apparent Time
Meridian Altitude observations of the sun could be taken without the need of a timepiece; most all other celestial observations were dependent on knowing the correct Local Apparent Time to within a few seconds. To take the meridian altitude of the sun, the observer watched the progress of the sun as it neared its daily apex, then, sighting with the octant or sextant, “tracked” it. The sun hangs for a few moments at its highest altitude before descending. At this point the observer locks the index arm in place, then reads the angle observed. This is the sun’s meridian altitude above the horizon.
Local Apparent Time is the time as shown by the sun at your location. When it is Local Apparent Noon the sun is due south of you, which is to say, on your meridian, and is (for all practical purposes) at its highest point in the sky. The time given by the chronometer for Local Apparent Noon, after a correction made for the sun’s changing declination and subtracted from 12:00:00, gives the error of the chronometer on Local Apparent Time for that particular noon. This time-check observation was called an “Equal Altitudes Observation of the Sun.”
Lewis took his Equal Altitudes observations as follows:
- He set out the artificial horizon.
- When the sun was nearly east or rising rapidly and had reached an altitude high enough to reduce the effects of refraction, he measured the altitude of the sun’s upper limb—that is, the upper edge of its disk—with the sextant and, simultaneously, had an assistant note and record the time shown by the chronometer. He then locked the index arm at the angle observed,
- Leaving the index arm locked at the angle observed, he called out to his assistant when the sun’s center reached that altitude. The assistant noted and recorded the time.
- When the sun’s lower limb reached that same altitude Lewis again called out to his assistant to note and record the time.
- Lewis then verified the altitude shown by the sextant’s index, recorded that altitude, then put the sextant away until the afternoon sun descended nearly to the altitude of the morning measurements.
- As the afternoon sun’s lower limb, center, and upper limb successively reached the altitude locked on the sextant’s index arm, Lewis called out to his assistant to note and mark the time.
From these data, the time that the chronometer would have shown at local noon could be calculated to within a second or so of noon—depending upon the accuracy of the observation. From observations taken the next day or a few days later, the chronometer’s daily and hourly rate of loss could be determined. Lewis and Clark took Equal Altitudes observations of the sun on the 27, 28 and 29 July 1804 to determine their chronometer’s error with respect to local time. These observations also provided the necessary information to determine the chronometer’s going rate (for Lewis’s chronometer this meant how much time the chronometer lost per day). Although the captains did not calculate the chronometer’s error while at the mouth of the Kansas River, Lewis would need to make these calculations to determine the magnetic declination and the longitude from the other observations he and Clark took there. The Equal Altitudes observations taken during those three days yield the following information:
| Date | Error, Local Apparent Time | Error, Local Mean Time | Daily Loss (Mean Time) |
|---|---|---|---|
| 27 | 7m 18.5s fast | 4m 43.6s fast | |
| 28 | 7m 08.4s fast | 4m 21.2s fast | 22.4 seconds |
| 29 | 7m 00.1s fast | 4m 00.9s fast | 20.3 seconds |
The difference of two seconds in the chronometer’s daily rate of loss does not necessarily reflect any change in its rate of loss at this location. It likely stems from the inaccuracy of the Equal Altitudes observations, themselves. The average daily loss of 21.4 seconds, however, certainly is significantly greater than the 15.5 seconds per day that Lewis recorded on 22 July 1804.[7]Moulton, ed., Journals, 2:412.
Longitude
The longitude that Lewis used to make his calculations for latitude and check his chronometer was an estimate. Jefferson’s instructions required that Lewis take observations to obtain the data needed to calculate the longitude. Lewis’s mainstay observation for longitude was called a Lunar Distance observation, or more commonly, a lunar. This observation required using the sextant to measure the angular distance between the moon and the sun or between the moon and a star. The time shown by the chronometer was noted and recorded for each angular-distance measurement. The calculations for longitude from the observation began by evaluating the distance-time data sets and discarding those that appeared spurious. Next the remaining distances were averaged as were the corresponding chronometer times. The average time then had to be corrected for chronometer error on true Local Apparent Time.
On the morning of 29 June 1804, the captains took six sets of observations of the angular distance between the moon and the sun with the sextant. Each consisted of eight measurements of the angular separation between the sun and moon’s nearest limbs and the time of each angular measurement. The moon, approaching its third quarter, was slowly closing the distance between itself and the sun to the east of it.
In order to evaluate the raw data, Lewis should have made a plot or graph of the times recorded versus the angular separation observed. From this plot the observation sets with the most consistent trends could be identified, using only those in the calculations for longitude. A plot of the data shows that Observation set No. 1 had the most consistent data, and Observation set No. 5 probably the second best.
Of all the celestial observations, the calculations for longitude were among the most complex, lengthy, tedious and subject to error. Lewis did not calculate the results of their observations during the expedition; we are going to make those calculations now. Using the data from Lunar Distance Observation set No.1 and the method for clearing[8]At the time of Lewis and Clark’s expedition several methods were available to “clear” the lunar. Clearing the lunar was the mathematical process by which the true distance between … Continue reading the Lunar Distance by Robert Patterson (see The Astronomy Notebook, 1803), the longitude by this observation is 94°26′ W. Using Jean Borda’s more rigorous method (1787) the longitude is 96°24’W.[9]Jean-Charles de Borda (1733-1799) was a French naval officer, mathematician, astronomer, and military engineer renowned in his time for his development of navigation instruments, and his studies of … Continue reading
Comparisons
The Expedition’s river survey together with the oldest detailed maps available and modern maps and aerial photos suggest that the Expedition’s camp at the mouth of Kansas River was at 94°36½’ West Longitude. The longitude derived from Observation set No. 1, averaging the results of Patterson’s and Borda’s methods is 94°25′ West. The captain’s longitude, thus, is 11½ arc minutes too far east of the longitude suggested above (94°36½’ West). At 53.8 miles per degree of longitude at 39°N, these 11½’ represent a distance of 10.3 miles. The Great Circle distance between Camp Dubois and the mouth of Kansas River is 242 miles. The 10-mile difference between the actual longitude and the longitude obtained from the captain’s celestial observation makes an error of 4.3%. By the captains’ river survey (estimated miles), the straight-line distance between Camp Dubois and the mouth of Kansas River is 271 miles—29 miles more than the actual 242 and an error of 12.1%. The longitude calculated from the captains’ Lunar Distance observations, though imprecise by modern standards, is much more nearly correct than the distance obtained from their estimated river miles. Jefferson clearly understood that this would be the case and that the longitudes derived from the captains’ celestial observations should be used to correct their compass-and-estimate river survey.
Inconsistencies
- The 1804 Missouri-Kansas junction point as I have identified it was at 39°07′ N, 94°36½’ W
- The junction point per the Expedition’s river survey corrected to True North is at 39°25’35″N, 95°07’54” W
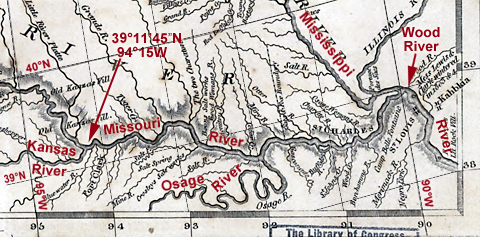
- The Lewis and Clark map of 1814 shows the junction point to be at 37°11’45” N, 94°15′ W (See map detail below.)
- The Expedition’s celestial observations put the junction point at 39°05’33” N, 94°25″ W[10]Lunar Distance Observation set No. 5 of 29 June 1804, produces a longitude of 94°17′ W. The average longitude from Lunar Distance Observation set No. 1 and No. 5 is 94°20½’, but the … Continue reading
Detail From Clark’s 1814 Map
To labels, point to the map.
Library of Congress, Geography and Map Division, Washington, D.C.
Cartographer Nicholas King prepared Clark’s final map for publication in Nicholas Biddle’s paraphrase of the captains’ journals, which was published in 1814. For some unknown reason King placed the mouth of the Kansas River 1¼° west of its location on Clark’s 1805 map. It appeared at 93°15′ on the 1806 map, and about 94°20′ on his 1810 revision.
Magnetic Declination
The needle of a magnetic compass points to True North only along a few ever-changing lines on the earth. A survey in the continental United States, based on Magnetic North, currently can depart from true north by as much as 15° West to as much as 20° East. This range of values was about the same for 1805. To correct a survey based on Magnetic North, the magnetic declination (or variation of the needle) must be known. The direction of True North can be found by several methods. In far northern latitudes during the winter the bearing of the sun can be taken at Local Apparent Noon (David Thompson usually did this). Another method is to take the bearing of the sun, its altitude and the chronometer time of the observation. Still another method is to observe the bearing of Polaris and the chronometer time of the observation. On 27 June 1804, the captains recorded the chronometer time for three observations of the bearing and altitude of the sun. These observations were intended to provide the data to calculate the magnetic declination at their camp at the mouth of Kansas River.
That same evening the captains also recorded the chronometer time for three observations of the bearing of Polaris, this also for magnetic declination. Lewis could calculate the true bearing of the sun from 1) the corrected time of the observation, 2) the latitude of the place of observation, 3) the declination of the sun for the estimated longitude and 4) the altitude of the sun’s center. The calculated values then could be compared to the magnetic bearings that were observed at those times. The differences then would be averaged to reduce random errors, and this average would be the magnetic declination for 1804 at the mouth of Kansas River by their sun observations. Lewis could calculate the true bearing of Polaris from a) the corrected average time of the Polaris observation, b) the declination of Polaris, c) the right ascension[11]The Right Ascension of a celestial body is the angle expressed in hours-minutes-seconds between that body and a point in the sky where the sun will be or was at the moment it crossed the celestial … Continue reading of Polaris, and d) the latitude of the place of observation. The difference between the calculated true bearing and the magnetic bearing that was observed is the magnetic declination by that observation.
| Observed Bearing | Object | Azimuth | Calculated Azumuth | Difference | Rounded to 1/2 |
|---|---|---|---|---|---|
| S81° E[12]“N81°E”: This bearing was either read or recorded incorrectly in the journals as S81°E; it should have been N81°E, which is used in the average here. | Sun | 099° | 091° 06′ | 07° 54′ W | 8° W |
| N81° E | Sun | 081° | 091° 06′ | 10° 06′ E | 10° E |
| S88° W | Sun | 268° | 277° 57′ | 09° 57′ E | 10° E |
| S89° W | Sun | 269° | 279° 19′ | 10° 19′ E | 10½° E |
| N7° 55′ W | Polaris | 352° 05′ | 001° 43′ | 09° 38′ E[13]“Polaris”: It was more difficult to take the bearing of Polaris with the circumferentor than it was to take the bearing of the sun. The value N7°55’W is the average of three … Continue reading | 09½° E |
| Average | 10° East | ||||
Clark’s Small-scale Maps
Clark prepared four maps that depicted the junction of the Missouri and Kansas rivers; these maps bear the dates 1805, 1806, 1810 and 1814 (Moulton, Atlas, maps 32a, 123, 125 and 126). Clark prepared the 1805 map while at Fort Mandan, drawing this map at a scale of 1 inch = 50 miles (1:3,168,000). His method of preparing this map not known. Certainly he did not replot the Expedition’s courses and distances taken while ascending the river (compare, for example, the area near the Big Bend of the Missouri in present-day South Dakota shown on Moulton’s Atlas, map 32a with that on Atlas map 22).
In comparing the coordinates shown on the five maps shown here, it may be helpful to remember that 1° of latitude always = 68.9 statute miles; at 38° N, 1° of longitude = 54.5 statute miles; at 39°N, 1° of longitude = 53.8 statute miles.
Detail From Clark’s 1805 Map
When the expedition’s courses and distances are plotted and matched to the expedition’s coordinates for Camp Dubois and to David Thompson’s coordinates for the Mandan villages (with adjustments for the latitudes the Expedition obtained along the way), the fit is much better than that shown on Clark’s 1805 map. In fact, the match between the Missouri River’s course produced from the Expedition’s river survey and that shown on modern maps is far better than any single map published until the map by the Missouri River Commission in 1893. Unfortunately, the 1805 map was not matched to known coordinates and, on that map, the mouth of the Kansas River is shown to be 86 miles East-by-North (azimuth 86°) from its actual location.
Detail from Clark’s 1806 Map
Clark’s map of 1806 probably also had an original scale of about 1 inch = 50 miles. That part of the map downstream from Fort Mandan appears to have been crudely traced or redrafted from a copy of the 1805 map. There are, however, major differences in longitude of many junctions, and the latitudes of other river junctions downstream from Fort Mandan often differ by 5 to 10 minutes (6 to 12 miles). The mouth of the Kansas is 71 miles East-by-North of its true location.
Detail From Clark’s 1810 Map
The 1810 map also was prepared at a scale of 1 inch = 50 miles, and although the 1806 map likely was used as a base, the 1810 map appears to have been completely redrafted. There is considerably more detail (much of it merely ornamentation) on many of the streams and, once again, latitudes and longitudes of many important points, such as the mouth of the Kansas River, have shifted. Here it appears 15 miles East of its true location.
Detail From Clark’s 1814 Map
The 1814 map was prepared by Samuel Lewis from a map by William Clark. The map was published at a scale of about 1:4,300,000 to 1:4,500,000 (about 1 inch = 1° of latitude). The map bears a strong resemblance to Clark’s 1810 map, but again, latitudes and longitudes of many important places differ from the preceding maps. Now the mouth of the Kansas is 21 miles northeast of its true location. The 1810 chart, it should be noted, was Clark’s master from which Samuel (no relation to Meriwether) Lewis made the drawing that the engraver used for the 1814 printing. The difference in the location of the Kansas was the result of an error in copying, and was not based on interpretation of any navigational data.
What does this array of charts add up to? As has been shown (see “Comparisons and Conclusions“), Lewis’s best observations, correctly recalculated, showed the Kansas joining the Missouri at 39°05’33” North, 94°25′ West. For comparison, the modern GPS coordinates where the Kansas touches the Missouri’s right bank are 39°06’54” North, 94°36’36” West. If Ferdinand Hassler had been able to detect Lewis’s errors, he could have shown the confluence to be only 10.5 statute miles west of its actual location. That would have been acceptable for a landmark such as this in 1804, or even at sea if a navigator were trying to find an island that rose, say, 250 feet above sea level. But if a ship’s navigator had to stay clear of hidden reefs at the same coordinates, this much error could be disastrous. Similarly, the geographical uncertainties reflected in this jumble of coordinates would be utterly unacceptable today. At the very least, land ownership would be a shambles, and it would be possible to land an airplane only under Visual Flight Regulations at either of the Kansas Cities.
These charts, then, show the magnitude of uncertainty in geographical thinking—understanding and misunderstanding—that prevailed during the early 19th century, and that remained to be resolved. Thomas Jefferson believed, to the end of his life, that it was imperative to have an absolutely accurate map of Louisiana, beginning with the Missouri River. Surely, one feels, with a little more effort and influence on his part he could have had what he wanted before 1814. It finally came to pass, however, with the building of transcontinental railroads after 1850, which required precise surveys based on exacting celestial observations and calculations.
Notes
| ↑1 | Magnetic declination, also called variation of the needle, is the difference in degrees between Magnetic North, which is the direction the needle of their magnetic compass pointed, and True North. The magnetic declination calculated from this and the other magnetic observations at this junction, together with those from other magnetic observations made along the expedition’s route, would allow the bearings in the captains’ river survey to be corrected from Magnetic North to True North. |
|---|---|
| ↑2 | Jefferson had instructed Lewis to base their estimates of distances traveled on waterways “by the compass the log-line & by time.”Lewis listed “Log line reel & log ship” among the equipment he purchased for the trip, but nowhere in the journals is their use confirmed. Donald Jackson, ed., Letters if the Lewis and Clark Expedition with Related Documents, 1783-1854, 2nd ed., 2 vols. (Urbana: University of Illinois Press, 1978), 1:61-62, 96. |
| ↑3 | Ferdinand Rudolph Hassler to Robert Patterson, 12 August 1810, in Donald Jackson, Letters of the Lewis and Clark Expedition with related documents 1783-1854 (Urbana: University of Illinois Press, 1978), 2:556-559. |
| ↑4 | See, for example: Richard Preston, “The Accuracy of the Astronomical Observations of Lewis and Clark,” Proceedings of the American Philosophical Society, vol. 144, no. 2 (June 2000), 168-191; Robert Bergantino, “Revisiting Fort Mandan’s longitude,” We Proceeded On, November 2001, 19-26.; Eileen Starr, 2001, “How the captains found latitude and (sometimes) longitude,” We Proceeded On , November 2001, 12-18; L. A. Rudner and Hans Heynau, “Revisiting Fort Mandan’s Latitude,” We Proceeded On, November 2001, 27-30; Bruce Stark, letter to the editor, We Proceeded On, August 2002. |
| ↑5 | Except at the summer and winter solstice, the sun’s declination—that is, its angular distance north or south of the celestial equator—is constantly changing. The Nautical Almanacs of Lewis and Clark’s day gave the sun’s declination only for Greenwich Apparent Noon. For an observation made at any other time or longitude, the sun’s declination had to be calculated. |
| ↑6 | See Clark’s map of 1805, Moulton, ed., Atlas, Map 32a. Clark probably prepared this map either by re-plotting their river survey at a smaller scale (1 inch = 100 miles) or redrafting the separate maps he had made of the Missouri from the Expedition’s river survey (1 inch = 6 miles). Despite often being hailed as a “cartographer,” Clark’s mapping abilities, though adequate for most tasks, often were compromised by time, equipment and training. On his map of 1805, the mouth of Kansas River is shown at 93° West Longitude, not 94° West as he should have shown it had he done his plotting carefully. |
| ↑7 | Moulton, ed., Journals, 2:412. |
| ↑8 | At the time of Lewis and Clark’s expedition several methods were available to “clear” the lunar. Clearing the lunar was the mathematical process by which the true distance between the moon and the sun or star was determined. For Lewis and Clark’s method of taking a lunar, this process involved calculating the altitude of the moon and sun (or star) and also calculating what their apparent altitudes would have been from the refraction and parallax associated with their altitude. Once these altitudes had been calculated the observer or mathematician followed a series of equations by which the moon and the second body were placed in their true position with respect to the center of the earth. Once this true distance was obtained (that is, once the lunar was cleared) the observer or mathematician would calculate what Greenwich Apparent Time would have been when this distance (or separation) occurred. Then, knowing the Greenwich Time of the separation and the local time of the observation, the longitude could be calculated. |
| ↑9 | Jean-Charles de Borda (1733-1799) was a French naval officer, mathematician, astronomer, and military engineer renowned in his time for his development of navigation instruments, and his studies of the size and shape of the Earth. He briefly participated in the American Revolutionary War. He published his rigorous method for clearing the lunar distance in 1787; competent authorities considered it to be the best solution to the problem. |
| ↑10 | Lunar Distance Observation set No. 5 of 29 June 1804, produces a longitude of 94°17′ W. The average longitude from Lunar Distance Observation set No. 1 and No. 5 is 94°20½’, but the data from Observation set No. 1 appear more coherent than those from No. 5, so weight ought to be given to the longitude derived from it. Observation sets 2, 3, 4 and 6 all contain too many spurious data pairs to warrant calculations. |
| ↑11 | The Right Ascension of a celestial body is the angle expressed in hours-minutes-seconds between that body and a point in the sky where the sun will be or was at the moment it crossed the celestial equator during the spring equinox. This point is called both the first point of Aries and the vernal equinox; it has a Right Ascension of 0h 00m 00.0s. the Right Ascension of the sun, moon, planets and brighter stars are calculated years in advance and published in a book called a Nautical Almanac, a copy of which was in the expedition’s portable library. The difference in Right Ascension between two bodies is the difference in time that they cross the upper meridian ( line due south from a person in the northern hemisphere). This difference, multiplied by 15, gives the angular separation of the two bodies referenced to the celestial equator. The celestial equator is essentially the plane of the earth’s equator projected to the celestial sphere, which, in turn, is the imaginary globe upon whose surface all celestial bodies are imagined to be affixed. |
| ↑12 | “N81°E”: This bearing was either read or recorded incorrectly in the journals as S81°E; it should have been N81°E, which is used in the average here. |
| ↑13 | “Polaris”: It was more difficult to take the bearing of Polaris with the circumferentor than it was to take the bearing of the sun. The value N7°55’W is the average of three observations, 8°W, 8°W and 7°45’W. If the circumferentor could be read only to the nearest½°, how did the captains obtain a bearing of N7°45’W for the third value of their observation with Polaris? |
Experience the Lewis and Clark Trail
The Lewis and Clark Trail Experience—our sister site at lewisandclark.travel—connects the world to people and places on the Lewis and Clark Trail.
Discover More
- The Lewis and Clark Expedition: Day by Day by Gary E. Moulton (University of Nebraska Press, 2018). The story in prose, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals: An American Epic of Discovery (abridged) by Gary E. Moulton (University of Nebraska Press, 2003). Selected journal excerpts, 14 May 1804–23 September 1806.
- The Lewis and Clark Journals. by Gary E. Moulton (University of Nebraska Press, 1983–2001). The complete story in 13 volumes.